Défloutage d'images : Un guide pour débutants

1. Introduction au défloutage d'images

Le défloutage d'image est le processus consistant à éliminer les distorsions présentes dans une image floue. Ce flou peut être causé par divers facteurs tels que le trémolo de l'appareil photo, le flou de mouvement, la turbulence atmosphérique ou des imperfections du système optique. L'objectif est de restaurer l'image originale nette à partir de sa version dégradée.

Figure 1 : Exemple de technologie de défloutage par l'IA montrant une comparaison avant et après

Le flou d'image se produit lorsque la fonction d'étalement du point (PSF) du système d'imagerie se convolue avec l'image originale. Le défi consiste à inverser ce processus afin de retrouver l'image nette. Les techniques modernes de défloutage vont des approches mathématiques traditionnelles à des méthodes sophistiquées basées sur l'apprentissage profond.

Figure 2 : Comparaison visuelle des différentes méthodes de défloutage d'images de visages

2. Modèle mathématique du flou d'image

Le modèle mathématique du flou d'image peut être exprimé comme suit :

Où :

• g(x, y) est l'image floue observée
• f(x, y) est l'image originale nette
• h(x, y) est la fonction d'étalement du point (PSF)
• n(x, y) est le bruit additif
• * désigne l'opération de convolution

3. Convolution : explication du processus de flou

La convolution est l'opération mathématique qui décrit comment la fonction d'étalement du point (PSF) affecte l'image originale pour produire un flou. Comprendre la convolution est essentiel pour saisir le mécanisme du flou et la manière de le corriger.

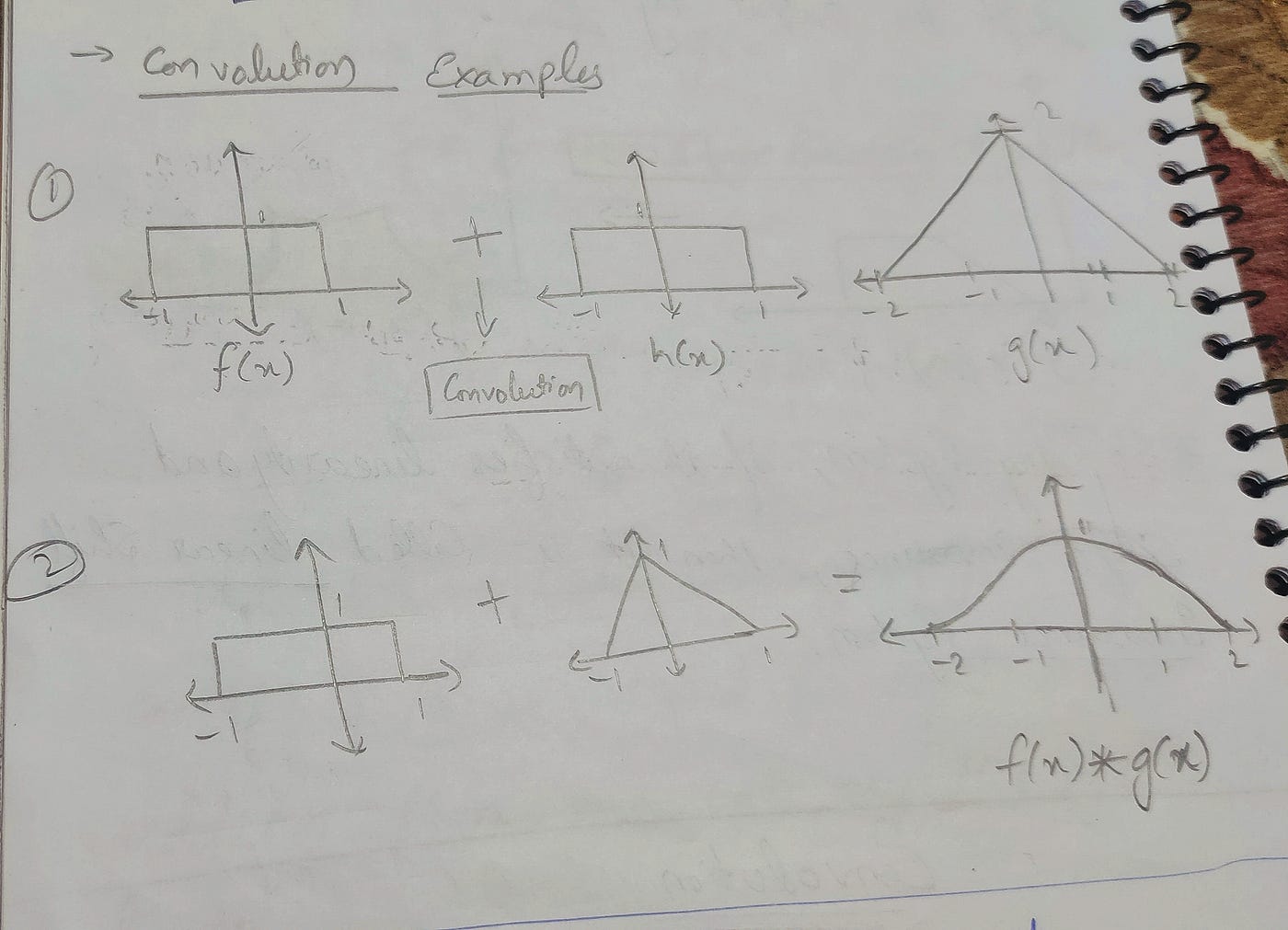
Figure 3 : Visualisation mathématique de l'opération de convolution en traitement d'image

L'opération de convolution applique la PSF à travers toute l'image, en calculant la somme pondérée à chaque position. Ce processus répartit l'énergie de chaque pixel sur les pixels voisins, créant ainsi l'effet de flou.

Figure 4 : Visualisation étape par étape du processus de convolution

4. Déconvolution : inverser le flou

La déconvolution est le processus inverse de la convolution, visant à retrouver l'image originale à partir de l'observation floue. Cela présente un défi mathématique en raison du bruit et de la nature mal posée du problème.

Figure 5 : Visualisation de l'opération de déconvolution

La difficulté en déconvolution réside dans le fait qu'il s'agit d'un problème inverse mal posé. De faibles quantités de bruit peuvent être fortement amplifiées, rendant l'inversion directe instable. C'est pourquoi des algorithmes sophistiqués sont nécessaires.

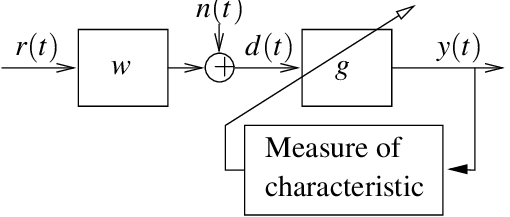
Figure 6 : Représentation schématique du système de convolution-déconvolution

5. Le rôle de la transformée de Fourier

La transformée de Fourier joue un rôle essentiel dans le défloutage d'images en convertissant l'opération de convolution dans le domaine spatial en une multiplication dans le domaine fréquentiel. Cette transformation simplifie l'analyse mathématique et permet d'obtenir des informations sur les caractéristiques fréquentielles du flou.

Figure 7 : Comparaison entre les représentations dans le domaine spatial et fréquentiel

Dans le domaine fréquentiel, la relation devient :

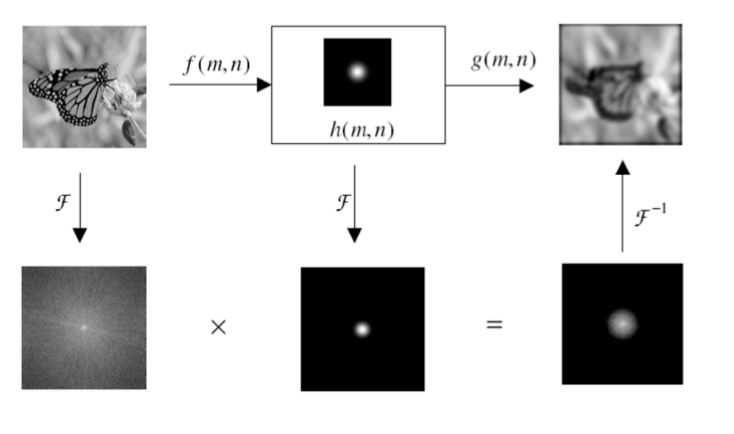
Figure 8 : Filtrage par transformée de Fourier dans le domaine fréquentiel

6. Techniques traditionnelles de défloutage

Les techniques traditionnelles de défloutage reposent sur des modèles mathématiques et des algorithmes d'optimisation. Ces méthodes ont été largement étudiées et constituent la base pour comprendre les approches modernes.

7. Filtre de Wiener

Le filtre de Wiener est un filtre linéaire optimal qui minimise l'erreur quadratique moyenne entre l'image estimée et l'image réelle. Il prend en compte à la fois le noyau de flou et les caractéristiques du bruit.

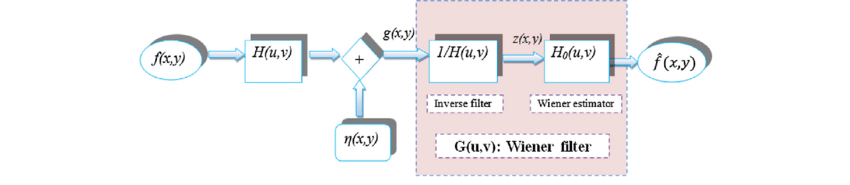
Figure 9 : Modèle mathématique du filtre de Wiener

La fonction de transfert du filtre de Wiener est donnée par :

Où :

• W(u, v) : Fonction de transfert du filtre de Wiener dans le domaine fréquentiel
• H(u, v) : Réponse en fréquence du système de dégradation (par exemple, flou)
• H*(u, v) : Conjugué complexe de H(u, v)
• |H(u, v)|² = H(u, v) ⋅ H^*(u, v) : Carré du module de la réponse en fréquence
• Sₙ(u, v) : Densité spectrale de puissance (DSP) du bruit
• S_f(u, v) : Densité spectrale de puissance (DSP) du signal ou de l'image originale non dégradée

8. Algorithme de déconvolution de Lucy-Richardson

L'algorithme de Lucy-Richardson est une méthode itérative basée sur l'inférence bayésienne et l'estimation du maximum de vraisemblance. Il est particulièrement efficace pour le défloutage d'images astronomiques et dans les applications de microscopie.

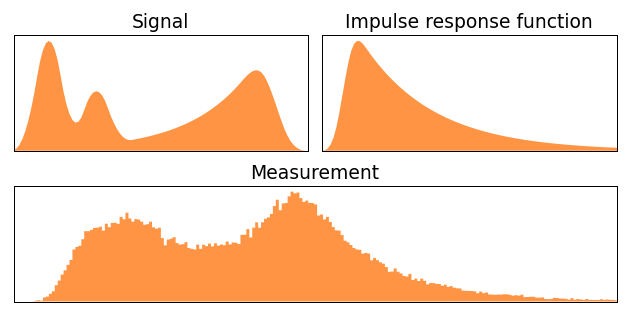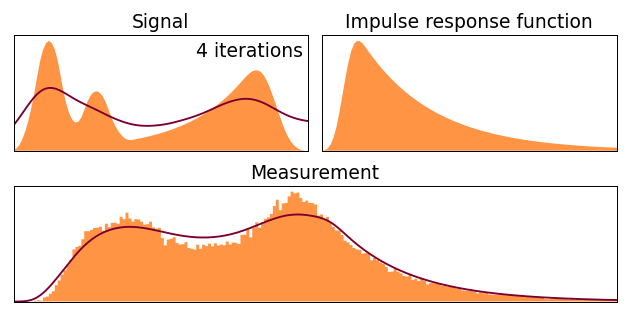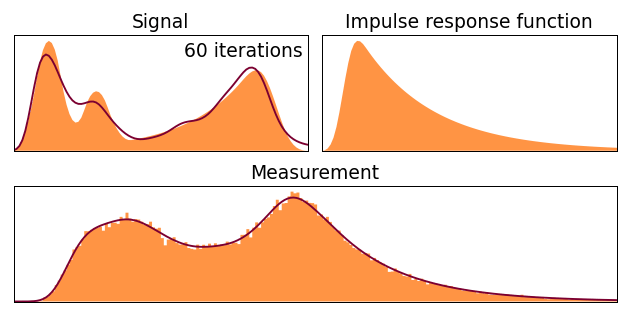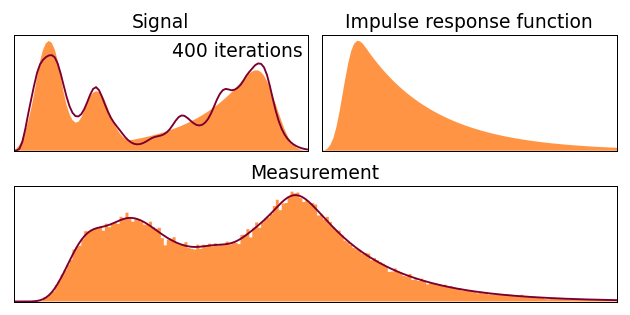
Figure 10 : Algorithme de déconvolution Richardson-Lucy en action

L'algorithme affine itérativement l'estimation à l'aide de la formule suivante :

Où :

• f^(k) : L'image estimée à l'itération k
• g : L'image observée (floue et possiblement bruitée)
• h : La fonction d'étalement du point (PSF), c'est-à-dire le noyau de flou
• h(-x, -y) : PSF inversée (c.-à-d. noyau retourné), utilisée dans l'étape de mise à jour
• * : Opérateur de convolution
• × : Multiplication pixel par pixel (échelle ponctuelle)
• / : Division pixel par pixel

Figure 11 : Comparaison entre la déconvolution aveugle et la méthode de Lucy-Richardson

9. Méthodes de déconvolution aveugle

La déconvolution aveugle s'attaque au cas difficile où à la fois l'image originale et le noyau de flou sont inconnus. Ces méthodes doivent estimer simultanément la fonction d'étalement du point (PSF) et l'image nette.

10. Techniques de défloutage basées sur l'apprentissage profond

L'apprentissage profond a révolutionné le défloutage d'images en apprenant des correspondances complexes entre les images floues et nettes directement à partir des données. Ces méthodes peuvent gérer divers types de flou et obtenir des résultats à l'état de l'art.

Figure 12 : Aperçu des approches d'apprentissage profond pour le défloutage d'images

11. Réseaux neuronaux convolutifs (CNN)

Les réseaux neuronaux convolutifs (CNN) constituent la base des systèmes modernes de défloutage d'images. Ils excellent dans l'apprentissage des hiérarchies spatiales et peuvent modéliser efficacement la relation complexe entre les images floues et les images nettes.

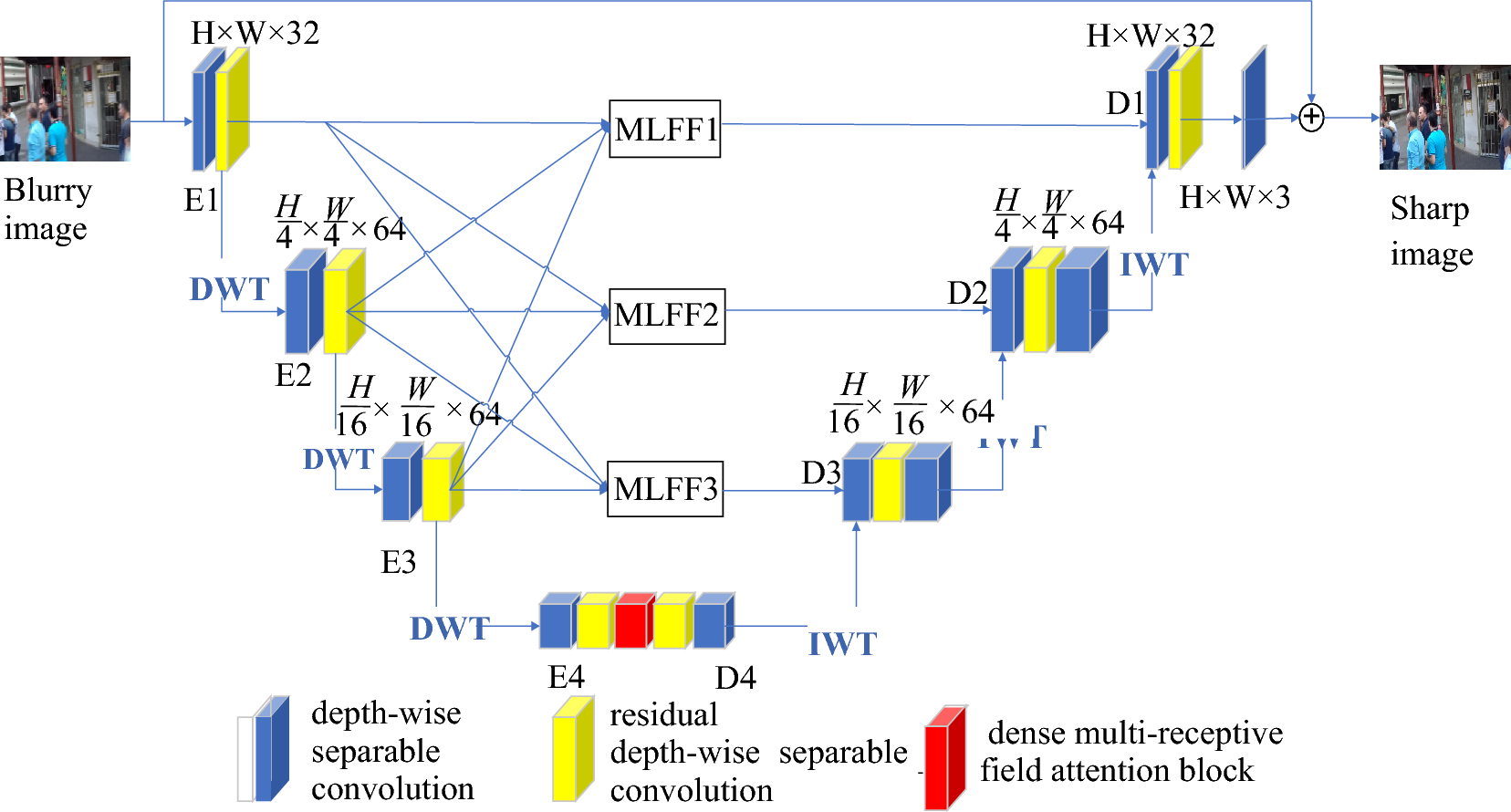
Figure 13 : Architecture U-Net adaptée au défloutage d'images

Les architectures CNN populaires pour le défloutage incluent :

• U-Net : Encodeur-décodeur avec connexions sautées
• ResNet : Connexions résiduelles pour les réseaux profonds
• DenseNet : Connexions denses pour la réutilisation des caractéristiques
• Réseaux multi-échelles : Traitement à plusieurs résolutions

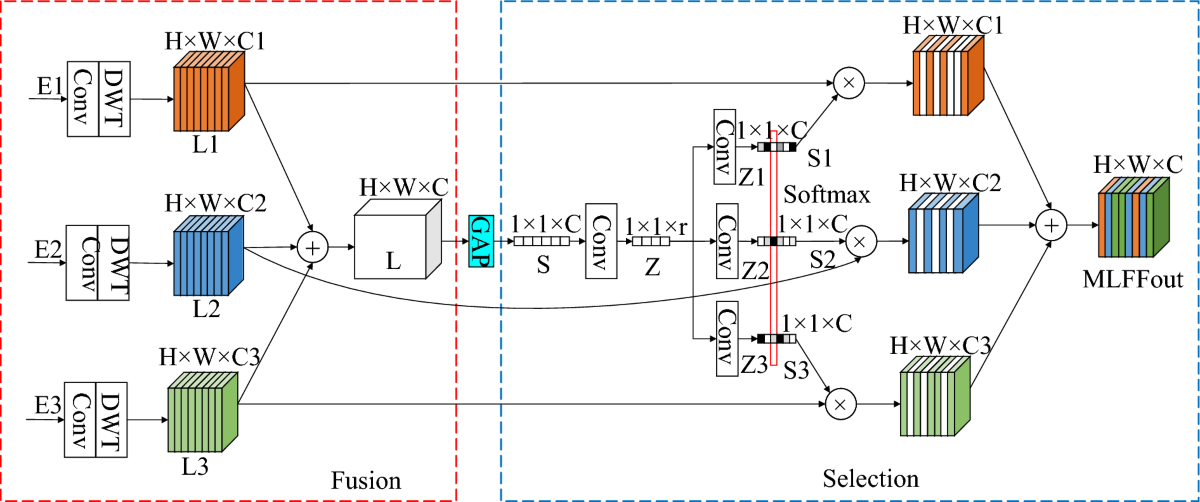
Figure 14 : Comparaison des résultats de différentes méthodes de défloutage basées sur les CNN

12. Réseaux antagonistes génératifs (GAN)

Les GAN (Generative Adversarial Networks) ont connu un succès remarquable dans le défloutage d'images en générant des images nettes réalistes du point de vue visuel. L'apprentissage adversaire permet de produire des images à la fois mathématiquement précises et esthétiquement attrayantes.

Figure 15 : Architecture de défloutage basée sur les GAN combinant CNN et GAN

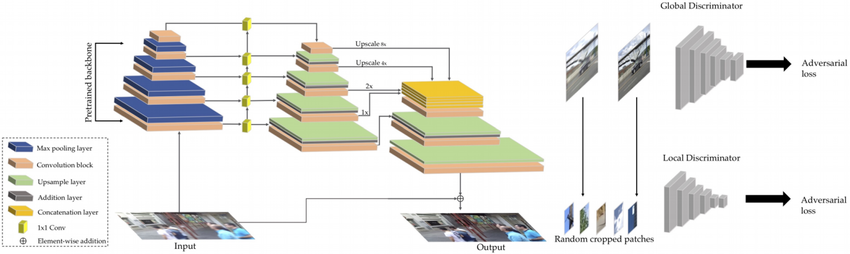
Figure 16 : Réseau de défloutage d'image unique basé sur l'architecture GAN

Avantages principaux des approches basées sur les GAN :

• Génèrent des textures et des détails réalistes visuellement
• Meilleure gestion des cas de flou sévère
• Amélioration des métriques de qualité visuelle
• Résilients face aux différents types de flou

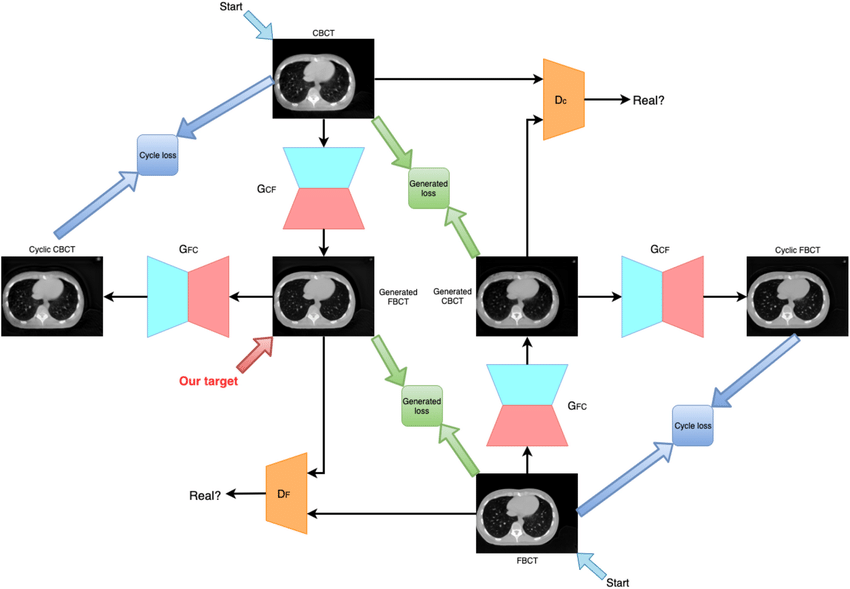
Figure 17 : Architecture de Cycle-Deblur GAN pour l'apprentissage non supervisé

13. Ensembles d'entraînement et fonctions de perte

Le succès des approches basées sur l'apprentissage profond dépend largement de données d'entraînement de haute qualité ainsi que de fonctions de perte adaptées, capables de mesurer à la fois la précision au niveau des pixels et la qualité perceptive.

14. Importance et applications du défloutage d'images

Le défloutage d'images trouve des applications variées dans de nombreux domaines, allant de la photographie amateur à l'imagerie scientifique et au diagnostic médical.

Figure 18 : Comparaison qualitative des différentes méthodes de défloutage sur des images réelles

15. Conclusion

Le défloutage d'images a évolué depuis les simples inversions mathématiques jusqu'à des systèmes avancés basés sur l'apprentissage profond. Le domaine continue d'évoluer grâce à de nouvelles architectures, stratégies d'entraînement et applications.

La combinaison des fondements mathématiques traditionnels et des techniques modernes d'apprentissage profond offre un cadre solide pour relever des défis de défloutage de plus en plus complexes. À mesure que la puissance de calcul augmente et que de nouveaux ensembles de données deviennent disponibles, nous pouvons anticiper des résultats encore plus impressionnants à l’avenir.